State-Augmented Linear Games with Antagonistic Error for High-Dimensional, Nonlinear Hamilton-Jacobi Reachability
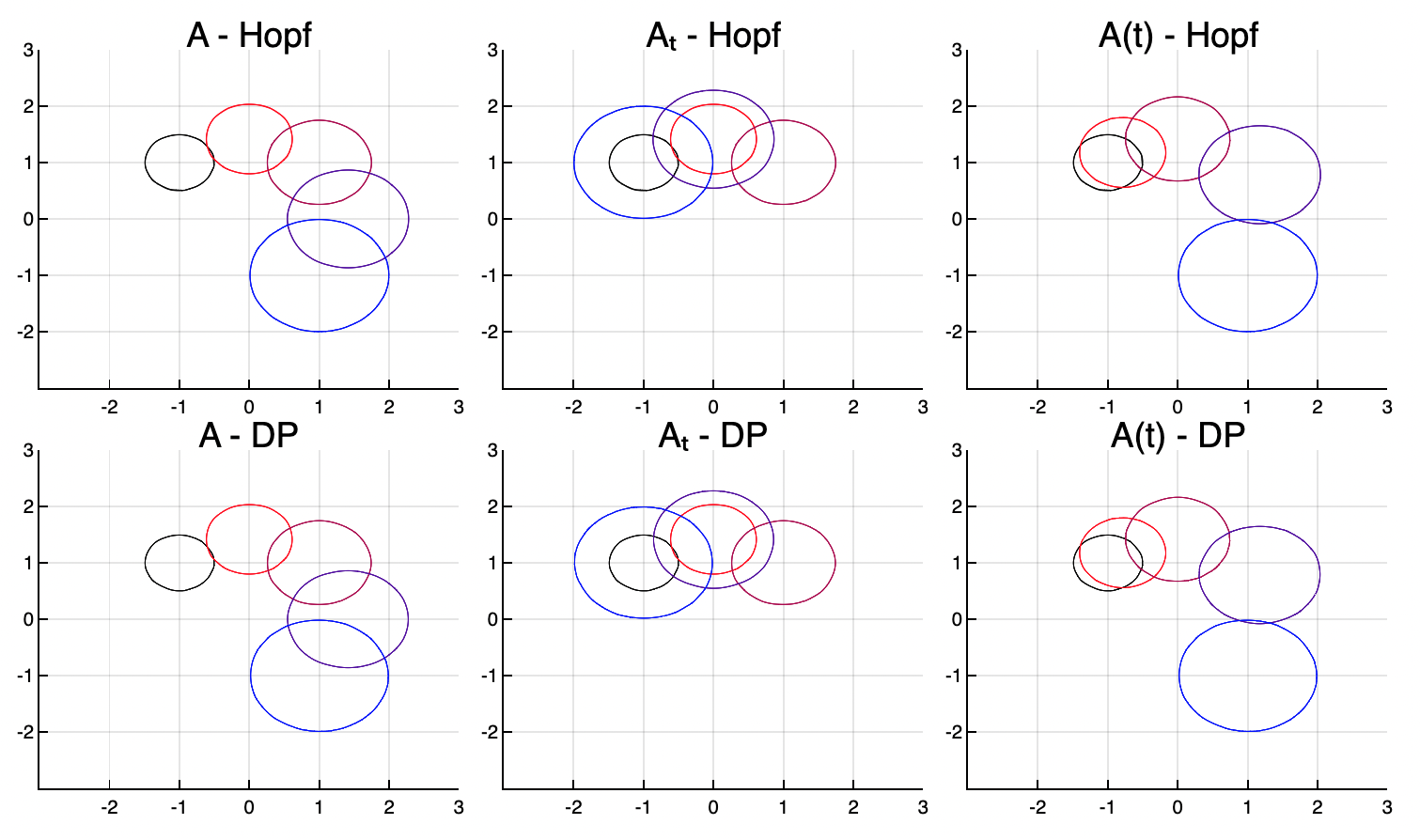
Hamilton-Jacobi Reachability (HJR) is a popular method for analyzing the liveness and safety of a dynamical system with bounded control and disturbance. The corresponding HJ value function offers a robust controller and characterizes the reachable sets, but is traditionally solved with Dynamic Programming (DP) and limited to systems of dimension less than six. Recently, the space-parallelizeable, generalized Hopf formula has been shown to also solve the HJ value with a nearly three-log increase in dimension limit, but is limited to linear systems. To extend this potential, we demonstrate how state-augmented (SA) spaces, which are well-known for their improved linearization accuracy, may be used to solve tighter, conservative approximations of the value function with any linear model in this SA space. Namely, we show that with a representation of the true dynamics in the SA space, a series of inequalities confirms that the value of a SA linear game with antagonistic error is a conservative envelope of the true value function. It follows that if the optimal controller for the HJ SA linear game with error may succeed, it will also succeed in the true system. Unlike previous methods, this result offers the ability to safely approximate reachable sets and their corresponding controllers with the Hopf formula in a non-convex manner. Finally, we demonstrate this in the slow manifold system for clarity, and in the controlled Van der Pol system with different lifting functions.
PDF Abstract