Directed Graph Embeddings in Pseudo-Riemannian Manifolds
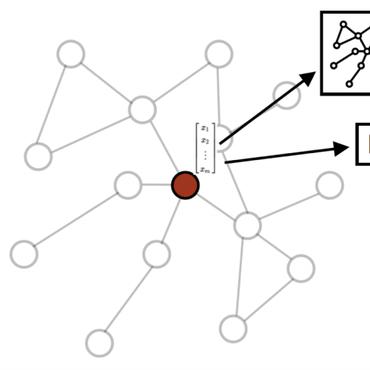
The inductive biases of graph representation learning algorithms are often encoded in the background geometry of their embedding space. In this paper, we show that general directed graphs can be effectively represented by an embedding model that combines three components: a pseudo-Riemannian metric structure, a non-trivial global topology, and a unique likelihood function that explicitly incorporates a preferred direction in embedding space. We demonstrate the representational capabilities of this method by applying it to the task of link prediction on a series of synthetic and real directed graphs from natural language applications and biology. In particular, we show that low-dimensional cylindrical Minkowski and anti-de Sitter spacetimes can produce equal or better graph representations than curved Riemannian manifolds of higher dimensions.
PDF Abstract